Abstract
This post is
concerned with the optimal design and development of Procedurally Generated
Planetary assets for video games on mobile devices. Successful
integration of procedural content for this technology is as yet, a heavily
under documented topic. Considering the current focus on mobile platforms as a
technological trend, and the implementation of video games with 3D graphics on
such platforms, it is only logical to seek optimised approaches to the
integration of such systems onto the technology.
The
topics discussed here within will focus primarily on the Quad Tree and Noise
approach to Procedural Planet Development with a build target of mobile phones
in mind.
- 1. Introduction 5
- 1.1 Procedural Content Generation (PCG) and the Video Games Industry 5
- 1.2 Optimization of PCG for Video Games 5
- 2. Procedural Planet Development 5
- 2.1 Noise Terrain 5
- 2.2 Fractal Terrain 6
- 2.3 Procedural Quad Tree Planets 7
- 3. Optimization for Mobile Devices 9
- 3.1 Issues on mobile 9
- 3.2 Optimization for System Performance 10
- 3.3 Optimization for User Experience 11
- 4. Conclusion 11
- 5. Bibliography 12
- 6. Figures 13
- 7. Glossary 15
1. Introduction
1.1
Procedural Content Generation
(PCG) and the Video Games Industry
Due to a rise in independent video game developments using 3rd party software for mobile devices (Fig.1, Helgason, 2014), and an industrial focus on on mobile technology, there are increasing opportunities for the implementation of Procedural Content Generation (PCG) in this domain. These techniques allow smaller teams to compete with much larger development studios (Carli, Bevilacqua, Pozzer, & d'Ornellas, 2011) through an automatic, or semi-automatic creation of game assets using computational algorithms. Optimization of such techniques for mobile devices would therefore be beneficial to the video games industry.
 |
1.2
Optimization of PCG for Video
Games
A common use of PCG in the video games industry is in the formation of computer generated terrains. These can be costly in terms of system performance, such as when using Online, Generate & Test (Togelius, Yannakakis, Stanley, & Brown, 2011, Smith, 2014) variations like Fractal Noise based Adaptive Subdivision within polygonal meshes (Mandlebrot, 1978) (Duchaineau et al, 1997) , discussed later in 2.2. To address this cost on mobile performance, this project will attempt to devise a set of optimized development practices for creating 3D planetary assets on such hardware using the aforementioned procedures. This will be approached by reviewing the development of a Procedural Quad Sphere (PQS) with an embedded Quad Tree node system and fractal levels of detail, for use on Googles Android OS via Unity3D. Furthermore, this post will include considerations on optimal player experience for such an environment as defined in the MDA framework of video games design (Hunicke, LeBlanc, & Zubek, 2004).
2.
Procedural Planet Development
2.1 Noise Terrain
To procedurally generate any graphical environment in computer science, a number of logical operations must be performed in tandem with a random or pseudo-random process. In the field of PCG, this is defined in the paper ‘Search-based Procedural Content Generation: A Taxonomy and Survey (Togelius, Yannakakis, Stanley, & Brown, 2011)’ as either Random Seed or Parameter Vector based. (Togelius, Yannakakis, Stanley, & Brown, 2011). The first definition refers to an input for a mathematical function that outputs values for generated content in a manner that has little to no parameter guidance. The vectors in the second refer to a manually guided trajectory for the procedure to follow using set parameters.
In creating terrain, we must first establish a Parameter Vector that meets certain criteria for its physical properties, such as the height of hills or colour of shading, using a seed value as the parameter. A common approach to this is to use Noise values, varying sequences of numbers derived from the Frequencies and Amplitudes of noise wavelengths (Fig. 2). Wavelengths can be of any dimension and are generated from an initial seed. In 3D examples their resultant values can be spread across the Cartesian world space of iterated generations of vertices forming a 3D mesh (usually quads), hence the term procedural generation (Fig. 3 & 4).
 |
 |
 |
2.2 Fractal Terrain
The effect within the mesh can be improved by using noise waves that
simulate the Fractal nature of real
world physical properties. A common approach method for this is in the use of Perlin Noise (Fig. 5, See Overleaf), a single wavelength formed of combined
wavelengths (Perlin, 1983). A suitable method of
using Perlin Noise for terrain is as
in music, where each additional wavelength is an Octave higher. An Octave is
a repeat wavelength but with double the frequency, known as Lacunacrity between
wavelengths. In addition, this frequency change is matched by dividing the
amplitude in half. This is known as the Persistance
of the wavelength. Lacunacrity and Persistence do not need to be exactly in
the power of 2, although it is quite common to do so.
 |
Using this method means
that different levels of detail can be present within meshes, dependent on
their vertex intensity. Combinations of other fractal approaches can further be
combined to one wavelength for perfecting detail even more (Fig. 6).
 |
Figure 6: Ridged Multi-Fractal
|
2.3
Procedural Quad Tree Planets
Given a mesh that will contain noise data for
terrains, in order to form a planetary sphere we require a topological
configuration within the mesh that does not polarize, as seen in many common
spherical primitives (Fig. 7). One
suitable topology known as a Quad Sphere
(Fig. 8), or PQS if produced procedurally, remains consistent with using quads
to contain noise data by forming a sphere out of a faceted cube. It is achieved
by normalizing each face of the cube toward it’s center.
 |
Figure 7:
Polarized Primitive Sphere
|
 |
Figure 8: Quad
Sphere
|
Additionally,
by maintaining quads, we can introduce a Quad
Tree to the mesh, a subdivision technique that allows level of detail to be
incorporated into geometry, based on the position of a relative object. In
context of the project, this allows excellent optimisation of system performace
due to rendering high details only where they are required. The idea is that a
parent node can divide by 4 into copies of itself, meaning the child nodes also
have the power to divide by 4. This process repeated forms divisional branches,
hence the use of the word tree. For example if we were to use a 16 x 16 quad,
we can divide that quad into equal proportional children due to the power of 2
(Fig. 9). The result across faceted quads create the
perfect scenario for including noise terrain on a planet for whichever view of
the surface can be seen (Fig. 10). In addition, due to the nature of fractal
noise, when combined with the normalization process, the child nodes display
deeper and deeper levels of detail. Usually the object used to invoke a branch is
the camera itself. Understanding of this system is derived from the work viewed
in Kerbal Space Program (Kerbal Space Program –
Squad, 2011).
 |
Figure 9: Quad Tree Divisions
|
 |
Figure 10: Quad Tree on a PQS
|
A quad
tree system used within procedural planet development can be further visualised
in figure 11 below.
 |
Figure 11: Quad Tree Diagram for
Procedural Planets
|
3.
Optimization for Mobile Devices
3.1 Issues on mobile
A system such as a procedural planet can easily overuse the available
resources of a mobile device through not adhering to the constraints of mobile
hardware. This may drastically lower framerates or worse, force a system out of
memory or bottleneck CPU processes, such as this example in Unity3D when attempting to apply more
and more textures to a procedurally generated Quad Tree.
Figure 12: Overloading of Processes through Planet Mismanagement
|
Furthermore, in attempting to run extensive procedures on mobile without optimization, aesthetic details can suffer loss of quality, hampering the visualization of the asset as an accurate simulation of a planet, as well as the overall user experience, such as this early attempt at reducing system cost.
 |
Figure 13: Lowest Quad Tree Simulation
|
3.2
Optimization for System
Performance
There
are a multitude of ways in which the generation process may be improved,
especially at the level of the graphics processing itself, however in a video
game engine there are several approaches in which a developer may consider performance
optimization. These
include:
1.
Ensuring that quads within the
mesh are of a suitable power of 2 to achieve minimal framerate during
subdivision of a node. For example a level 3 (quads of 8 x 8) sphere to remain
around a suitable target framerate of 30fps. See 3.3 for testing.
2.
Separating the generation of
mesh data from the application to the mesh in order to reduce bottle-necking of
the CPU (Fig. 14), especially during Quad Tree based node subdivision. This can be achieved by using a Coroutine method to delay the data applcation and
caching of parent nodes as a simple approach (Fig. 15). However this can impair the visual effect if misapplied.
 |
Figure 14: Bottleneck Spike as shown
in Unity3D Profiler
|
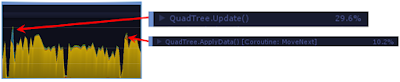 |
Figure 15: Separation of Generation
and Application Processes
|
3. Setting a custom target frame rate by disabling V-Sync operations and changing the applying a custom float to a targetFrameRate variable. In Unity3D this can easily be applied with the following code:
int customFPSTarget = #;
QualitySettings.vSyncCount = 0;
if (Application.targetFrameRate != customFPSTarget)
Application.targetFrameRate = customFPSTarget;
3.3 Optimization Testing
Optimization
Test for approach 1: Highest complexity in mesh that can achieve a smooth rate of frames per second
during proximity based subdivision.
Overview
Increases in mesh complexity
levels will be tested for frames per second (FPS) and process performance as
well as VBO size, Mesh MB size and garbage collection allocation to find the
most optimal topology that subdivides within 25-35 FPS. Use of cube primitive
(labelled ‘Approach Object’) as
camera parent with physics based motion used to induce distance and proximity
based subdivision process within generated ‘CubeSphere’.
Conditions
CubeSphere
|
Approach Object
|
Position:
0, 0, 400
Rotation:
0, 0, 0
Scale:
50, 50, 50
Tested
Parent Node: 1
Maximium
Quadtree Level: 4
|
Start
Position: 0, 0, 0 (Origin)
Rotation:
0, 0, 0
Scale:
1, 1, 1
Approach
Speed (C# Class): UnityEngine.Rigidbody.AddForce (transform.forward * 250)
|
Control Measure = 150 fps
Average
System Specification (Available Testing Equipment)
CPU
|
Intel®
Xeon® CPU E5-1620 v2 @ 3.70GHz 3.69 GHz
|
GPU
|
Nvidia
Quadro K4000 3GB Graphics
|
RAM
|
HP
16.0 GB DDR3 (Max: 1066MHz)
|
Operating
System
|
Windows
8.1 Enterprise 64-bit Operating System, x64-based processor
|
DirectX
Version
|
DirectX
9
|
Mobile
Handset
|
Sony
Xperia Mobile Phone SP
|
Orthographic Top View of Testing Environment & Profiler using Unity3D
VPN = Vertices
per Node
TPN = Triangles
per Node
Quad Tree division at Levels 1, 2 & 3 are deemed optimal. This refers to cubespheres with a 2x2, 4x4 and 8x8 divide quadtree face.
 |
| Table 1: Results |
3.3
Optimization for User
Experience
In keeping with the MDA Framework of Video Games Design (Hunicke, et al., 2004), a developer must remember that when a
procedural planet is packed as part of a product, a user may not share the same
perception of that system. For instance, a player may simply see the
environment as just the Game Stage (Smith,
2014) and seek play in a Game as
Challenge rather than invoking, what would be anticipated, Game as Discovery (Hunicke, et al.,
2004).
To counter this, the system
must somehow relate to how the player would wish to traverse it. In his PhD
Thesis ‘Engineering
Emergence: Applied Theory for Games Design’ (Dormans, 2012, 189-190) Joris
Dormans contrasts PCG against the notion of Fractal
stories discussed by Marie-Laure Ryan in her book ‘Narrative as Virtual Reality: Immersion and Interactivity in Literature
and Electronic Media’. He can be quoted:
“Where branching stories build towards different, predesigned endings
along pre-designed paths, the fractal story transforms itself to accommodate
many different paths that essentially
lead towards the same goal” - (Dormans, 2012)
This refers to designs in
narrative in which more and more detail are added dependant on the trajectory
through a games Probability Space,
the possible states that a game may be in (Adams & Dormans, 2012). In
considering Procedural Planets with a Quad Tree system, for each successive
division within the terrain, the game state may include, remove, increase or
decrease certain resources within a games internal economy, a theoretical
construct designed to visualise play flow using numerical values (Dormans,
2012).
4. Conclusion
The
optimizations presented within this document require further research to be
considered effective. Furthermore, several other approaches towards procedural
planet development currently exist which may render these techniques obsolete,
such as the use of Tessellation Shaders to induce LOD rather than scripted Quad
Trees. However it can be confidently stated that using third party software to
develop procedural content for mobile is a logical direction for any current
video game developer. Advancements in technology will push such concepts more
and more into the limelight, potentially overriding most other development
practices, such as the prototype procedural game play and mechanic software Ludoscope (Dormans, 2012) developed by Joris
Dormans. Now is the prime time to get involved.
5. Bibliography
- Adams, E. & Dormans, J., 2012. Game Mechanics: Advanced Game Design. Berkeley: New Riders; 1st edition.
- Carli, D. M. D., Bevilacqua, F., Pozzer, C. T. & d'Ornellas, M. C., 2011. A survey of procedural content generation techniques suitable to game development. Salvador, Institute of Electrical and Electronics Engineers, p. 1.
- Dormans, J., 2012. PhD Thesis: Engineering Emergence: Applied Theory for Games Design, Amsterdam: Creative Commons.
- Duchaineau, M. et al., 1997. ROAMing Terrain: Real-time Optimally Adapting Meshes. Los Alamitos, CA, IEEE Computer Society Press, pp. 81-88.
- Google Android Operating System, 2015. Android. [Online]
- Available at: http://www.android.com/
- Google Open Source Code, 2014. libnoise-dotnet. [Online]
- Available at: https://code.google.com/p/libnoise-dotnet/
- Helgason, D., 2014. Unite Keynote 2014. Seattle, Unity3D.
- Hunicke, R., LeBlanc, M. & Zubek, R., 2004. MDA: A Formal Approch to Game Design and Game Research. San Jose, CA, AAAI Press.
- Julia, G., 1918. Mémoire sur l'itération des fonctions rationnelles. Journal de Mathématiques Pures et Appliquées, pp. 47-246.
- Krieger, D. H., 2014. The Mandlebrot Set, s.l.: MIT, Numberphile.
- Mandelbrot, B., 1978. MandelbrotSet.. [Online].
- Member:12pt, 2014. Student Game Dev: C# Voxel Tutorial. [Online]
- Available at: http://forum.unity3d.com/threads/tutorial-procedural-meshes-and-voxel-terrain-c.198651/
- Perlin, K., 1983. m_perlin. [Online]
- Available at: http://freespace.virgin.net/hugo.elias/models/m_perlin.htm
- Ryan, M.-L., 2001. Narrative as Virtual Reality: Immersion and Interactivity in Literature and Electronic Media. New Ed edition (3 Oct 2003) ed. Baltimore, MD: The Johns Hopkins University Press.
- Smith, G., 2014. Understanding Procedural Content Generation: A Design-Centric Analysis of the Role of PCG in Games. New York, ACM.
- Squad, 2011. Kerbal Space Program, s.l.: Squad.
- Togelius, J., Yannakakis, G. N., Stanley, K. O. & Brown, C., 2011. Search-based Procedural Content Generation: A Taxonomy and Survey. Copenhagen, IEEE.
6. Figures
Figure 1: David Helgason - Unite Keynote Conference 2014 .......................................... 5
Figure 2: 1D Noise Wavelength & Noise Values ............................................................. 6
Figure 3: 2D & 3D Noise .................................................................................................. 6
Figure 4: Noise Based Mesh ............................................................................................. 6
Figure 5: Combined Perlin Wavelength ........................................................................... 7
Figure 6: Ridged Multi-Fractal ......................................................................................... 7
Figure 7: Quad Sphere ...................................................................................................... 7
Figure 8: Polarized Primitive Sphere ................................................................................ 7
Figure 9: Quad Tree Divisions .......................................................................................... 8
Figure 10: Quad Tree on a PQS ........................................................................................ 8
Figure 11: Quad Tree Diagram for Procedural Planets ..................................................... 8
Figure 12: Overloading of Processes through Planet Mismanagement ............................ 9
Figure 13: Low Aesthetic Simulation ............................................................................... 9
Figure 14: Bottleneck Spike as shown in Unity3D Profiler ........................................... 10
Figure 15: Separation of Generation and Application Processes .................................... 10
7. Glossary
- Adaptive Subdivision – Geometry that can intelligently divide in specific ways under different conditions.
- Arbitrarily Large – In Mathematics, a set of values that increases in magnitude.
- Bounded – In Mathematics, a set of values that are restricted within a range.
- Complex Number – In Mathematics, a number derived from the relative position of an Imaginary Number across the Complex Plane.
- Complex Plane – In Mathematics, a Cartesian Coordinate system contrasting Real Numbers against Imaginary Numbers.
- Fractal – A geometric state in which each part has the same statistical characteristics as the whole.
- Generate & Test – In Procedural Generation, a system that generates data and checks to see if the result has met certain conditions.
- Imaginary Number – In Mathematics, a number that is mathematically impossible.
- MDA Framework – In Video Games Design and standing for Mechanics, Dynamics & Aesthetics, an approach to formally understand the development of a videogame as a single process for determining player experience, rather than individual processes combined together.
- Online – In Procedural Generation, a system that generates data during run time.
- Parameter Vector – In Procedural Generation, a guided method of generating data within method parameters.
- PCG – Standing for Procedural Content Generation, a system that automatically, or semi-automatically creates content for a product.
- Probability Space – The potential states of a game inherited by player trajectory.
- Procedural Quad Sphere (PQS) – In Procedural Generation, a procedurally generated, faceted cube forming a sphere with no geometric poles
- Quad Tree – A method of division that uses nodes that can divide by 4 into repeat nodes with the same divisional properties.
- Random Seed – In Procedural Generation, a generation of values in which a seeded outcome is not guided in any way.
- Real Number – In Mathematics, any number that is mathematically possible.

